5y 1 6x 4y 10
fonoteka
Sep 23, 2025 · 5 min read
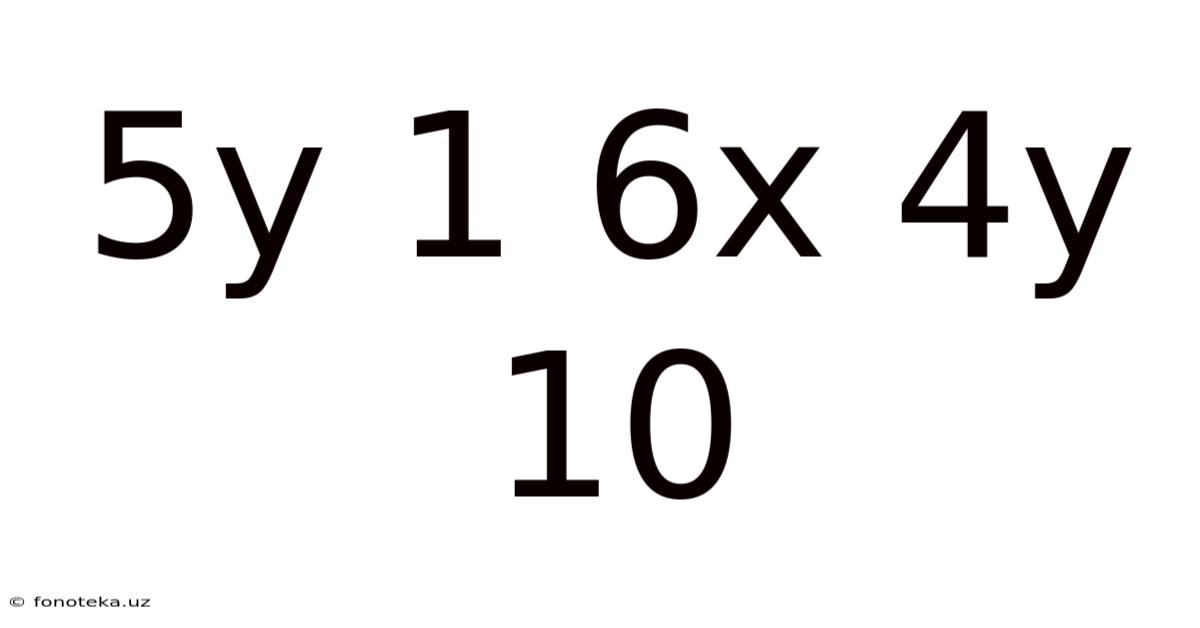
Table of Contents
Decoding the Mathematical Expression: 5y + 1 = 6x + 4y + 10
This article delves into the mathematical expression 5y + 1 = 6x + 4y + 10, exploring its solution, various approaches to solving it, and the underlying mathematical concepts involved. Understanding this seemingly simple equation opens doors to a deeper appreciation of algebraic manipulation and problem-solving strategies. We'll explore this equation step-by-step, catering to readers of all mathematical backgrounds, from beginners grappling with basic algebra to those seeking a refresher on equation solving techniques.
Introduction: Understanding the Equation
The equation 5y + 1 = 6x + 4y + 10 represents a linear equation in two variables, x and y. This means that the equation describes a straight line on a coordinate plane. Solving this equation doesn't yield a single solution for x and y, but rather an infinite number of ordered pairs (x, y) that satisfy the equation. These ordered pairs represent points that lie on the line defined by the equation. Our aim is to manipulate the equation to express one variable in terms of the other, thereby revealing the relationship between x and y.
Step-by-Step Solution: Simplifying and Rearranging
Our first step involves simplifying the equation by combining like terms. Observe that both sides of the equation contain terms with 'y'. Let's gather these terms on one side and the terms with 'x' and constant terms on the other.
-
Subtract 4y from both sides: This leaves us with 5y - 4y + 1 = 6x + 10.
-
Simplify: This simplifies to y + 1 = 6x + 10.
-
Subtract 1 from both sides: This isolates 'y', giving us y = 6x + 10 - 1.
-
Further simplification: This leads to the final simplified form: y = 6x + 9.
This equation now expresses y explicitly in terms of x. For any given value of x, we can calculate the corresponding value of y that satisfies the original equation. This equation represents a linear relationship with a slope of 6 and a y-intercept of 9.
Graphical Representation: Visualizing the Solution
The equation y = 6x + 9 can be easily graphed on a Cartesian coordinate system. The y-intercept, 9, tells us that the line crosses the y-axis at the point (0, 9). The slope of 6 (which can be written as 6/1) indicates that for every 1 unit increase in x, y increases by 6 units. This allows us to plot additional points and draw the line representing all possible solutions to the equation.
Plotting several points, such as (0, 9), (1, 15), (-1, 3), etc., and connecting them will visually represent the infinite number of solutions. Every point on this line corresponds to an (x, y) pair that satisfies the original equation 5y + 1 = 6x + 4y + 10.
Alternative Solution Methods: Exploring Different Approaches
While the method above is straightforward, other approaches can be used to solve or manipulate this equation. For instance:
-
Expressing x in terms of y: Instead of isolating y, we could isolate x. Starting from y = 6x + 9, we can subtract 9 from both sides to get y - 9 = 6x. Then, dividing both sides by 6, we get x = (y - 9) / 6. This form is equally valid and expresses x as a function of y.
-
Using matrices (for more advanced learners): While not necessary for this specific equation, linear equations can also be solved using matrix methods. This approach becomes particularly useful when dealing with systems of multiple linear equations. However, for a single equation with two variables, it's generally an overkill.
Understanding the Underlying Mathematical Concepts
The solution and manipulation of this equation highlight several core mathematical concepts:
-
Linear Equations: The equation is a classic example of a linear equation, characterized by its first-degree variables (x and y are raised to the power of 1).
-
Variables and Constants: The equation uses variables (x and y), representing unknown quantities, and constants (1, 10, 5, 4, 6), representing fixed numerical values.
-
Algebraic Manipulation: The process of solving the equation involves applying algebraic rules, such as adding, subtracting, multiplying, and dividing both sides of the equation by the same value to maintain equality.
-
Equivalent Equations: Each step in our solution process generates an equation equivalent to the original one; they all represent the same line on the coordinate plane.
-
Slope-Intercept Form: The final simplified form, y = 6x + 9, is in the slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept. This form is highly useful for understanding the graphical representation of the equation.
Frequently Asked Questions (FAQ)
Q: Is there only one solution to this equation?
A: No. A linear equation in two variables has infinitely many solutions, representing all the points on the line defined by the equation.
Q: What does the slope of 6 mean in the context of this equation?
A: The slope of 6 signifies that for every one-unit increase in the x-value, the y-value increases by six units. It represents the rate of change of y with respect to x.
Q: Can this equation be solved without simplifying first?
A: Yes, but it would be more complex. Simplifying by combining like terms makes the process much more efficient and less prone to errors.
Q: What if the equation had more variables?
A: If the equation contained more variables, you would need more equations to find a unique solution for each variable. This would involve solving a system of linear equations.
Q: What are some real-world applications of solving linear equations?
A: Linear equations have countless real-world applications. They're used in various fields such as physics (modeling motion), economics (analyzing supply and demand), engineering (designing structures), and computer science (creating algorithms).
Conclusion: A Deeper Dive into Linear Algebra
The seemingly simple equation 5y + 1 = 6x + 4y + 10 provides a valuable introduction to the world of linear algebra. Through step-by-step simplification, we arrived at a more manageable form, y = 6x + 9, revealing the linear relationship between x and y. This process underscores the importance of algebraic manipulation, the understanding of variables and constants, and the visual representation of solutions through graphing. Furthermore, it lays the foundation for tackling more complex algebraic problems and systems of equations. This comprehensive exploration serves as a starting point for further investigation into the fascinating world of mathematics. The ability to solve and interpret such equations is a critical skill applicable across numerous disciplines, solidifying its importance in both academic and practical contexts.
Latest Posts
Latest Posts
-
Posterior View Of Superficial Muscles
Sep 23, 2025
-
What Is Not A Mineral
Sep 23, 2025
-
Europe During The Renaissance Map
Sep 23, 2025
-
Heartcode Acls Answers 2025 Pdf
Sep 23, 2025
-
Ap World Unit 2 Test
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5y 1 6x 4y 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.