Factor X 2 8x 15
fonoteka
Sep 15, 2025 · 6 min read
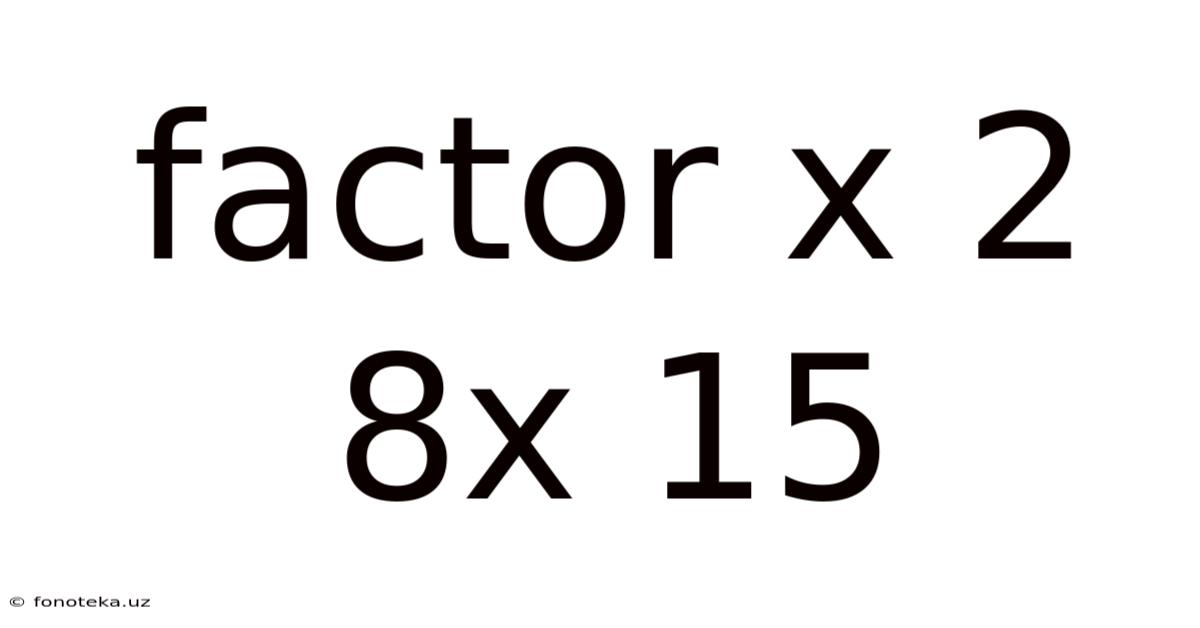
Table of Contents
Factoring the Quadratic Expression: x² + 8x + 15
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This article will guide you through the process of factoring the specific quadratic expression x² + 8x + 15, explaining the steps involved, the underlying mathematical principles, and addressing common questions. We'll explore different methods and provide a deeper understanding of this important algebraic concept.
Introduction
The expression x² + 8x + 15 is a trinomial—a polynomial with three terms. Factoring this trinomial means rewriting it as a product of two simpler expressions, usually two binomials. This process is crucial for solving quadratic equations, simplifying algebraic fractions, and understanding various mathematical concepts. This article will break down the factoring process step-by-step, making it accessible even to beginners. We'll also delve into the reasons why the factoring method works, providing a solid foundation for your algebraic understanding.
Method 1: Finding Factors of the Constant Term
This method is often the quickest and easiest way to factor simple quadratic trinomials like x² + 8x + 15. It relies on identifying two numbers that satisfy specific criteria:
-
Identify the constant term: In our expression, x² + 8x + 15, the constant term is 15.
-
Find factors of the constant term that add up to the coefficient of the x term: We need to find two numbers that multiply to 15 and add up to 8 (the coefficient of the x term). Let's list the factor pairs of 15:
- 1 and 15
- 3 and 5
- -1 and -15
- -3 and -5
-
Identify the correct pair: The pair 3 and 5 satisfies both conditions: 3 * 5 = 15 and 3 + 5 = 8.
-
Write the factored form: Using the numbers we found, we can write the factored form of the quadratic expression as: (x + 3)(x + 5).
Verification:
To verify our factoring, we can expand the factored form using the FOIL method (First, Outer, Inner, Last):
(x + 3)(x + 5) = x² + 5x + 3x + 15 = x² + 8x + 15
This confirms that our factoring is correct.
Method 2: The AC Method (for more complex quadratics)
While the previous method works well for simpler trinomials, the AC method is a more general approach that can be applied to more complex quadratic expressions, even those with a coefficient in front of the x² term. Although unnecessary for x² + 8x + 15, understanding this method provides a more robust understanding of factoring.
Let's illustrate this method with a slightly more complex example, and then show its application to our original problem. Consider the quadratic 2x² + 7x + 3.
-
Identify a, b, and c: In the quadratic ax² + bx + c, a = 2, b = 7, and c = 3.
-
Find the product ac: ac = 2 * 3 = 6
-
Find factors of ac that add up to b: We need two numbers that multiply to 6 and add up to 7. These numbers are 1 and 6.
-
Rewrite the middle term: Rewrite the middle term (7x) using the two numbers we found: 2x² + 6x + x + 3
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 3) + 1(x + 3)
-
Factor out the common binomial: Notice that (x + 3) is a common factor in both terms. Factor it out: (x + 3)(2x + 1)
Now, let's apply the AC method to our original problem, x² + 8x + 15.
-
Identify a, b, and c: a = 1, b = 8, c = 15
-
Find the product ac: ac = 1 * 15 = 15
-
Find factors of ac that add up to b: The factors 3 and 5 multiply to 15 and add up to 8.
-
Rewrite the middle term: x² + 3x + 5x + 15
-
Factor by grouping: x(x + 3) + 5(x + 3)
-
Factor out the common binomial: (x + 3)(x + 5)
As you can see, both methods yield the same result: (x + 3)(x + 5).
Explanation of the Underlying Mathematical Principles
The success of these factoring methods hinges on the distributive property of multiplication. The distributive property states that a(b + c) = ab + ac. When we factor a quadratic, we're essentially reversing this process. We're finding the original 'a', 'b', and 'c' that when multiplied together using the distributive property, result in our original trinomial.
The AC method employs a clever strategy of rewriting the middle term to enable grouping and factoring. This works because adding zero to an expression doesn't change its value. By cleverly adding and subtracting the same quantity, we manipulate the expression into a form that allows for factoring by grouping.
Solving Quadratic Equations Using Factoring
Factoring is a powerful tool for solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0. To solve a quadratic equation using factoring, follow these steps:
-
Write the equation in standard form: Ensure the equation is in the form ax² + bx + c = 0.
-
Factor the quadratic expression: Factor the left side of the equation using the methods described above.
-
Set each factor equal to zero: Use the zero product property, which states that if the product of two factors is zero, then at least one of the factors must be zero.
-
Solve for x: Solve each resulting equation for x.
Example:
Let's solve the quadratic equation x² + 8x + 15 = 0.
-
Standard Form: The equation is already in standard form.
-
Factor: We've already factored x² + 8x + 15 as (x + 3)(x + 5).
-
Set each factor to zero: (x + 3) = 0 or (x + 5) = 0
-
Solve for x: x = -3 or x = -5
Therefore, the solutions to the equation x² + 8x + 15 = 0 are x = -3 and x = -5.
Frequently Asked Questions (FAQs)
-
What if the quadratic expression cannot be factored easily? If you can't find factors easily, you can use the quadratic formula to find the roots (solutions) of the corresponding quadratic equation. The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a.
-
Can all quadratic expressions be factored? Not all quadratic expressions can be factored using integers. Some require the use of irrational or complex numbers.
-
What is the difference between factoring and simplifying? Factoring rewrites an expression as a product of simpler expressions, while simplifying aims to reduce an expression to its most compact form. Factoring is often a step in simplifying.
-
Why is factoring important? Factoring is crucial for various mathematical operations, including solving equations, simplifying fractions, and analyzing graphs of quadratic functions. It’s a fundamental building block of advanced algebra and calculus.
Conclusion
Factoring the quadratic expression x² + 8x + 15, resulting in (x + 3)(x + 5), is a straightforward process once you understand the underlying principles. Whether you use the simpler method of finding factors of the constant term or the more general AC method, the key is to find two numbers that multiply to the constant term and add up to the coefficient of the x term. This skill is essential for progressing in algebra and mastering more complex mathematical concepts. By understanding the reasoning behind the methods and practicing regularly, you’ll build a solid foundation in algebra and confidently tackle more challenging quadratic expressions. Remember to always verify your factoring by expanding the factored form to ensure it matches the original expression. This article has aimed to provide a comprehensive understanding of this important algebraic technique. Continue practicing, and you'll become proficient in factoring quadratics in no time!
Latest Posts
Latest Posts
-
Exclusive Right To Sell Listing
Sep 15, 2025
-
To Cause Cancer Proto Oncogenes Require
Sep 15, 2025
-
A Business Overhead Expense Policy
Sep 15, 2025
-
What Was The Nebraska Act
Sep 15, 2025
-
Quotes Fahrenheit 451 Page Numbers
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.