The Diagram Represents 6x2-7x 2
fonoteka
Sep 16, 2025 · 5 min read
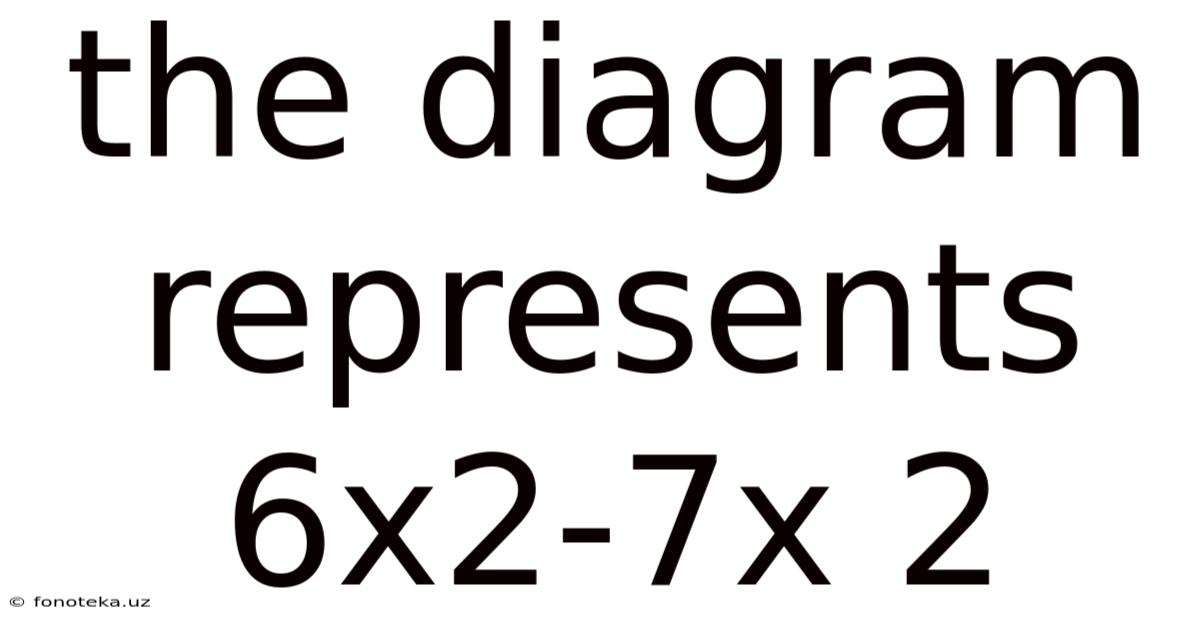
Table of Contents
Deconstructing 6x² - 7x²: A Deep Dive into Quadratic Expressions
This article explores the seemingly simple algebraic expression, 6x² - 7x², providing a comprehensive understanding of its components, simplification, and broader implications within the realm of algebra, particularly quadratic equations. We'll move beyond the basic solution to uncover the underlying mathematical principles and explore real-world applications. Understanding this seemingly simple expression is fundamental to grasping more complex algebraic concepts.
Introduction: Understanding the Building Blocks
The expression 6x² - 7x² represents a quadratic expression. Let's break down the individual components:
-
x²: This signifies the variable x raised to the power of 2. In simpler terms, it means x multiplied by itself (x * x). This is the quadratic term, defining the expression's type.
-
6x² and 7x²: These are terms. Each term is a combination of a coefficient (the number in front of the variable) and a variable raised to a power. In our example, 6 and 7 are the coefficients. They tell us how many x²'s we have.
-
-: The minus sign indicates subtraction. This operation dictates how we combine the terms.
Step-by-Step Simplification: Combining Like Terms
The key to simplifying 6x² - 7x² lies in the concept of like terms. Like terms are terms that have the same variable raised to the same power. In this case, both 6x² and 7x² are like terms because they both contain x². This allows us to combine them using simple arithmetic.
Here's how to simplify:
-
Identify Like Terms: We've already identified 6x² and 7x² as like terms.
-
Combine Coefficients: We perform the subtraction operation indicated by the minus sign: 6 - 7 = -1.
-
Write the Simplified Expression: The simplified expression is -1x², or more concisely, -x².
The Simplified Expression: -x²
The simplified form, -x², is still a quadratic expression. The coefficient is now -1, indicating that we have a negative one x². This means the parabola represented by this expression opens downwards. This seemingly small change significantly affects the graph of the function and its properties.
Visual Representation: Graphing Quadratic Equations
Understanding the graphical representation of quadratic equations is crucial. The expression -x² represents a parabola. Let's explore its characteristics:
-
Parabola: The graph of a quadratic equation is always a parabola – a U-shaped curve.
-
Vertex: The vertex is the highest or lowest point on the parabola. For -x², the vertex is at the origin (0,0). Since the coefficient is negative, the parabola opens downwards, meaning the vertex is a maximum point.
-
Axis of Symmetry: The parabola is symmetric about a vertical line called the axis of symmetry. For -x², this line is the y-axis (x = 0).
-
Roots (or x-intercepts): The roots are the points where the parabola intersects the x-axis (where y = 0). For -x², the only root is at x = 0.
Expanding the Concept: More Complex Quadratic Expressions
While 6x² - 7x² is a relatively simple example, understanding its simplification paves the way for tackling more complex quadratic expressions. Consider the following examples:
-
3x² + 5x² - 2x²: This expression involves multiple like terms. Following the same principle, we combine the coefficients: 3 + 5 - 2 = 6. The simplified expression is 6x².
-
4x² - 3x + 2x² + x: This expression contains both x² and x terms. We can only combine like terms: (4x² + 2x²) + (-3x + x) = 6x² - 2x. Note that we cannot combine x² and x terms as they are not like terms.
-
(2x + 3)(x - 1): This is a factored quadratic expression. Expanding this expression using the FOIL method (First, Outer, Inner, Last) results in a quadratic equation that can be simplified.
- First: 2x * x = 2x²
- Outer: 2x * -1 = -2x
- Inner: 3 * x = 3x
- Last: 3 * -1 = -3
- Combining like terms: 2x² + x - 3
Applications of Quadratic Equations in Real-World Scenarios
Quadratic equations are not just abstract mathematical concepts; they have numerous real-world applications across various fields:
-
Physics: Projectile motion (e.g., the trajectory of a ball thrown in the air) is described by quadratic equations.
-
Engineering: Quadratic equations are used in structural design and calculations.
-
Business and Economics: Quadratic functions can model profit, revenue, and cost functions. Finding the maximum or minimum point of a quadratic function is essential in optimizing business decisions.
-
Computer Graphics: Parabolas and other quadratic curves are used in computer graphics to create smooth, curved shapes.
Frequently Asked Questions (FAQ)
-
Q: What happens if the coefficients are not integers?
A: The process remains the same. You simply add or subtract the coefficients as usual, even if they are decimals or fractions.
-
Q: Can I simplify expressions with different powers of x?
A: No. You can only combine like terms, meaning terms with the same variable raised to the same power. For instance, you cannot simplify 3x² + 2x.
-
Q: What if the expression involves more than one variable?
A: The principles remain the same, but you can only combine like terms that have identical variables raised to the same power. For instance, 5xy² and -2xy² are like terms and can be simplified.
Conclusion: Mastery Through Understanding
The seemingly simple expression 6x² - 7x² offers a gateway to understanding the broader world of algebra and quadratic equations. By breaking down the expression into its components, understanding like terms, and practicing simplification, you build a strong foundation for tackling more complex algebraic problems. The application of these principles extends far beyond the classroom, demonstrating the practical relevance of mathematics in various fields. Remember, mastering the fundamentals is key to unlocking more advanced concepts and solving real-world challenges. Keep practicing, and your understanding of quadratic expressions will deepen with each exercise.
Latest Posts
Latest Posts
-
Dental Instruments Names And Pictures
Sep 16, 2025
-
Adp 7 0 Board Questions
Sep 16, 2025
-
The Respiratory Membrane Consists Of
Sep 16, 2025
-
Principles Of Real Estate 1
Sep 16, 2025
-
A Coworker Didnt Clean Walmart
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about The Diagram Represents 6x2-7x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.