The Prefix Blank Means Axis
fonoteka
Sep 16, 2025 · 7 min read
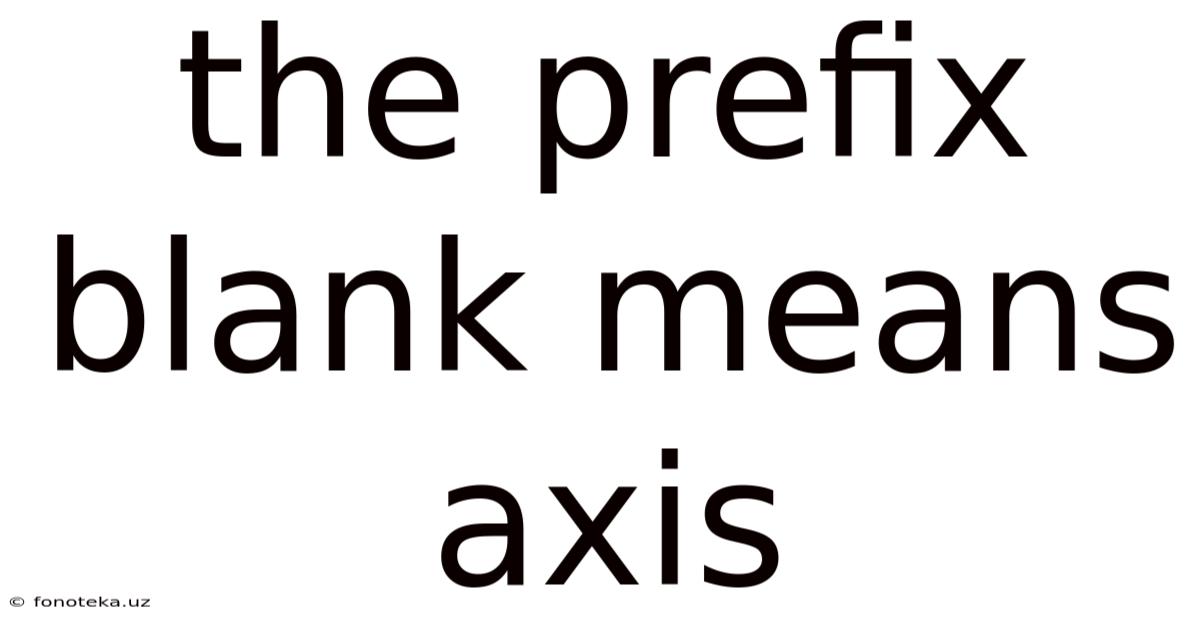
Table of Contents
The Prefix "Blank" and its Surprising Connection to Axes: Exploring the Etymology and Applications
The prefix "blank," often associated with emptiness or a lack of information, might seem an unlikely candidate for connection to something as precise and structured as an axis. However, a deeper dive into etymology reveals a fascinating and somewhat counterintuitive link. Understanding this connection requires exploring the evolution of the word "blank" and its surprising applications in various technical fields, where its meaning subtly shifts to represent a fundamental reference point or a neutral state from which measurements and actions originate. This article will delve into the historical roots of "blank," demonstrate its usage in contexts relating to axes, and explore its broader implications in various scientific and technical disciplines.
The Etymological Journey of "Blank"
The word "blank" traces its roots back to the Old French word "blanc," meaning "white." This connection to whiteness is key to understanding its evolution. In medieval times, blank pages in manuscripts were literally white, signifying an absence of writing. This visual representation of emptiness evolved into the more abstract meaning of lacking information or content. Think of a "blank stare," a "blank canvas," or a "blank check"—all referencing a state of emptiness or potentiality.
However, this seemingly simple history reveals a more nuanced interpretation when applied to the concept of axes. The "blank" state, in this context, isn't about an absolute void but rather a neutral, un-marked reference point. It represents the origin, the zero point, or the starting line from which other measurements and orientations are defined.
"Blank" as a Reference Point: Applications in Coordinate Systems
The concept of a "blank" axis becomes clear when considering coordinate systems. Imagine a Cartesian plane. The x and y axes intersect at the origin (0,0). This origin point can be considered a "blank" state, a neutral position from which all other points are defined relative to it. Moving along the x-axis, positive values extend to the right, negative to the left. Similarly, the y-axis extends upward and downward. The axes themselves, particularly the origin, provide a "blank" template upon which coordinates are plotted. Any point on the plane is merely a deviation from this central, "blank" axis intersection.
This principle extends to other coordinate systems as well, such as polar coordinates or spherical coordinates. In each, a central, "blank" point or axis acts as the reference frame, from which all other measurements are calculated. This "blank" axis isn't devoid of meaning; rather, it's the foundation upon which the entire system is built.
Blank Axes in Engineering and Manufacturing
The concept of a "blank" axis finds practical application in engineering and manufacturing. Consider the design and construction of mechanical parts. Many designs involve rotation around an axis. The axis of rotation often serves as a "blank" reference point for design calculations. Measurements are made relative to this axis—distances from the axis, angles of rotation around the axis, etc. The axis itself is often considered the neutral position, the unchanged reference point amidst the changing geometries of the rotating component.
Similarly, in the field of Computer-Aided Design (CAD), the design process often starts with defining a set of axes within a 3D workspace. These axes represent a "blank" state, a neutral reference frame upon which the designer builds the 3D model. The designer will add elements, adjust positions, and perform various operations, all relative to these fundamental "blank" axes. This "blank" state allows for precise control over the geometry and location of components within the design.
Blank Axes in Data Visualization and Analysis
The concept of a "blank" axis also emerges in the context of data visualization and analysis. A graph, for example, might have x and y axes representing independent and dependent variables. The intersection of these axes—the origin (0,0)—can be viewed as a "blank" state, representing the point of zero value for both variables. Data points are then plotted relative to this "blank" axis, showing deviations from the zero point. This "blank" axis, therefore, provides the necessary framework for interpreting the data displayed.
Data analysis itself often involves defining reference points or axes. In statistical analysis, for instance, the mean or average value of a dataset can serve as a "blank" reference point. Deviations from this "blank" central point, represented by standard deviation, provide valuable insights into the distribution of the data. The "blank" point, in this instance, represents the average or neutral state, from which the distribution around the average is measured.
The "Blank" Slate Metaphor: From Emptiness to Potentiality
The connection between "blank" and axes can be further explored through the common metaphor of the "blank slate." While traditionally associated with a clean, empty surface ready for writing or painting, the "blank slate" can be interpreted in the context of axes as a neutral state of potentiality. Just as a blank slate holds the potential for any number of drawings or writings, a "blank" axis provides the potential for any number of spatial locations or measurements. It is a starting point, not an empty nothingness. It is the foundation upon which a structure or a system is built.
Beyond the Cartesian Plane: Extending the Concept of "Blank" Axes
The idea of a "blank" axis extends beyond simple two-dimensional Cartesian planes. In three-dimensional space, the x, y, and z axes intersect at a single point – the origin, providing a three-dimensional “blank” reference frame. This concept is crucial in areas such as 3D modeling, robotics, and computer graphics. The positioning of objects and the execution of movements are entirely reliant on referencing these three “blank” axes.
Further, the concept extends even to higher dimensional spaces, often used in mathematical and physics modelling. While visualizing higher dimensions is difficult, the conceptual basis of a "blank" axis as a neutral reference point remains a crucial part of defining and working with these spaces. These axes serve as the foundation for defining vector spaces, tensor fields, and other complex mathematical structures.
FAQ: Clarifying Common Questions about "Blank" Axes
Q: Is a "blank" axis truly blank or does it have inherent properties?
A: While the term "blank" suggests emptiness, in the context of axes it represents a neutral or zero-point reference, not a void. It possesses inherent properties – such as direction and orientation – that are essential for defining the coordinate system.
Q: Can a "blank" axis change its position?
A: The position of a "blank" axis, particularly the origin in a coordinate system, is usually fixed within a given frame of reference. However, the entire coordinate system itself can be transformed or rotated. This transformation would shift the position of the axes, but the concept of a "blank" axis as the reference point remains.
Q: Are there instances where a "blank" axis isn't necessary?
A: While most coordinate systems rely on "blank" axes, there might be specific cases where a relative reference point might be sufficient. However, the use of "blank" axes provides a consistent and universally understood frame of reference for unambiguous measurements and descriptions.
Q: How does the concept of a "blank" axis relate to other mathematical concepts?
A: The concept is fundamental to linear algebra, vector calculus, and many other branches of mathematics. It relates directly to concepts like vectors, matrices, and transformations, all of which rely on the "blank" axis as the foundation for their operations.
Conclusion: Reframing the Understanding of "Blank"
The prefix "blank," typically associated with emptiness, takes on a new and profound meaning when applied to axes. It represents not a void, but a crucial reference point—a neutral state from which measurements and orientations are defined. From simple Cartesian planes to complex multi-dimensional systems, the concept of a "blank" axis underlies many scientific and technical applications. Understanding this nuance helps us appreciate the subtle but significant role of this seemingly simple prefix in a vast array of fields, redefining our comprehension of its connotation beyond mere emptiness to a powerful concept of neutrality and origination. The idea of a "blank" axis, while seemingly simple, unlocks a deep understanding of coordinate systems and how we represent and manipulate spatial information in various fields. Its importance in scientific and engineering applications underscores the power of seemingly simple words to hold complex meanings within specific contexts.
Latest Posts
Latest Posts
-
Somatosensory Cortex Ap Psychology Definition
Sep 16, 2025
-
Why Does Macbeth Kill Banquo
Sep 16, 2025
-
Calc 1 Final Exam Review
Sep 16, 2025
-
Field Observations Ap Human Geography
Sep 16, 2025
-
Urban Hierarchy Ap Human Geography
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about The Prefix Blank Means Axis . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.